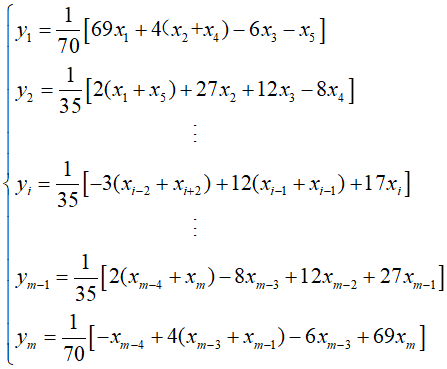小师的Blog
0%

Python离散数据处理

发表于 更新于 分类于
本文字数： 20k 阅读时长 ≈ 18 分钟

Python数据处理

Scipy数学处理模块

https://docs.scipy.org/doc/scipy/reference/index.html

模块 功能
scipy.cluster 矢量量化 / K-均值
scipy.constants 物理和数学常数
==scipy.fftpack== 傅里叶变换
==scipy.integrate== 积分程序
scipy.interpolate 插值
==scipy.io== 数据输入输出，支持多种类型文件读写
scipy.linalg 线性代数程序
scipy.ndimage n维图像包
scipy.odr 正交距离回归
scipy.optimize 优化
==scipy.signal== 信号处理
scipy.sparse 稀疏矩阵
scipy.spatial 空间数据结构和算法
scipy.special 任何特殊数学函数
scipy.stats 统计

numpy模块

https://numpy.org/doc/stable/reference/index.html#reference

数值积分

梯形规则：

梯形积分只有1阶代数精度。

1
scipy.integrate.trapezoid(y, x=None, dx=1.0, axis=-1)

辛普森规则：

对于等间距的奇数个样本，如果函数是 3 阶或更小的多项式，则结果是精确的。如果样本不是等间距的，那么只有当函数是 2 阶或更小的多项式时，结果才是准确的。

1
2
3
4
5
scipy.integrate.simps(y, x=None, dx=1, axis=-1, even='avg')
# even = {‘avg’, ‘first’, ‘last’}
# avg：平均first和last两个结果 默认参数
# first：对前N-2个区间使用Simpson规则，最后一个区间使用梯形规则
# last：对后N-2个区间使用Simpson规则，第一个区间使用梯形规则

测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from scipy.integrate import simps
from scipy.integrate import trapz
import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0,4)
y = x ** 2
print(x)
print(y)
z= trapz(y,x)
print(z)

z= simps(y,x,even='last')
print(z)

plt.plot(x,y)
plt.show()

输出

1
2
3
4
[0 1 2]
[0 1 4]
3.0
2.6666666666666665

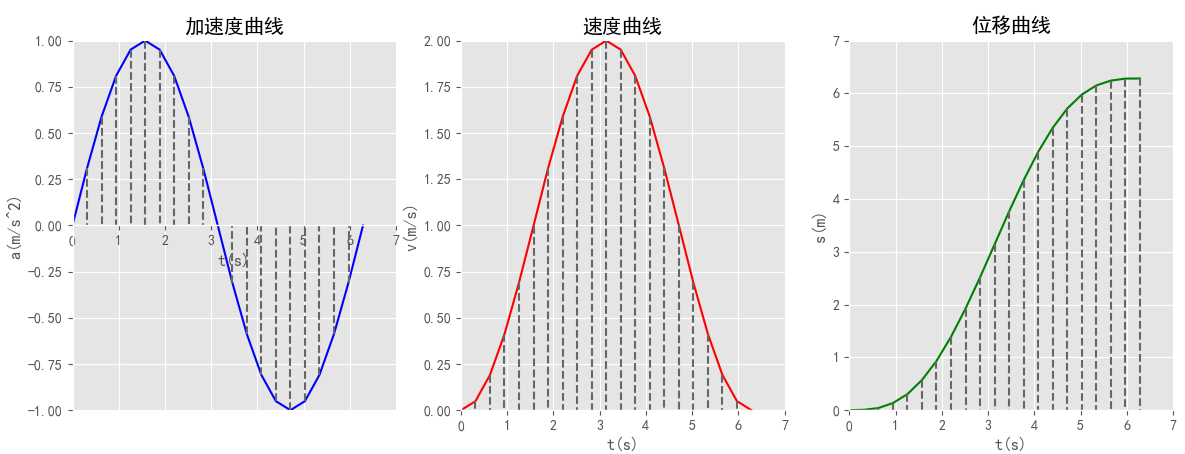
加速度计积分

image-20220308115529357

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
from scipy.integrate import simps
import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示符号

x = np.arange(0, 21) * 2 * np.pi / 20
# y = np.sin(x) + np.random.rand(x.size) * 0.1
y = np.sin(x)

v = []
for i in range(len(x)):
    v.append(simps(y[:i + 1], x[:i + 1]))

s = []
for i in range(len(x)):
    s.append(simps(v[:i + 1], x[:i + 1]))

print(y)
print(v)
print(s)

# matplotlib官方提供了五种不同的图形风格，分别是：bmh、ggplot、dark_background、fivethirtyeight 和 grayscale
plt.style.use('ggplot')
# plt.figure() # 创建一个画图窗口，可配置num图名、figsize画布大小、facecolor背景色、edgecolor边缘色
plt.subplot(1, 3, 1)  # 将画布划分为1行3列
plt.title("加速度曲线")  # 设置图表的标题
plt.ylabel('a(m/s^2)')  # 设置坐标轴的标签
plt.xlabel('t(s)')
plt.xlim(0, 7)  # 设置坐标轴的刻度范围
plt.ylim(-1, 1)
# plt.xticks(np.linspace(0,10,5),rotation=45) # 设置坐标轴刻度信息，rotation表示旋转
# plt.legend() # 设置显示图例，loc参数设置图例显示的位置
# 移动坐标轴，spines为脊梁，即4个边框
ax = plt.gca()  # get current axis 得到当前的坐标轴
ax.spines['right'].set_color('none')  # 设置右‘脊梁’消失掉
ax.spines['top'].set_color('none')  # 设置上‘脊梁’消失掉
ax.xaxis.set_ticks_position('bottom')  # 底部‘脊梁’设置为X轴
ax.yaxis.set_ticks_position('left')  # 左部‘脊梁’设置为Y轴
ax.spines['bottom'].set_position(('data', 0))  # 底部‘脊梁’移动位置，通过值来选择，x轴值为o的位置
ax.spines['left'].set_position(('data', 0))  # 左部‘脊梁’移动位置，y轴值为0的位置
# 绘制折线图，参数color表示颜色，label图例，linestyle曲线风格，linewidth曲线宽度，marker标记点样式，markersize标记点大小
plt.plot(x, y, color='blue')
for i in range(y.size):
    plt.plot([x[i], x[i]], [y[i], 0], color='#666666', linestyle='--')

plt.subplot(1, 3, 2)
plt.title("速度曲线")
plt.ylabel('v(m/s)')
plt.xlabel('t(s)')
plt.xlim(0, 7)  # 设置坐标轴的刻度范围
plt.ylim(0, 2)
ax = plt.gca()  # get current axis 得到当前的坐标轴
ax.spines['right'].set_color('none')  # 设置右‘脊梁’消失掉
ax.spines['top'].set_color('none')  # 设置上‘脊梁’消失掉
plt.plot(x, v, color='red')
for i in range(y.size):
    plt.plot([x[i], x[i]], [v[i], 0], color='#666666', linestyle='--')

plt.subplot(1, 3, 3)
plt.title("位移曲线")
plt.ylabel('s(m)')
plt.xlabel('t(s)')
plt.xlim(0, 7)  # 设置坐标轴的刻度范围
plt.ylim(0, 7)
ax = plt.gca()  # get current axis 得到当前的坐标轴
ax.spines['right'].set_color('none')  # 设置右‘脊梁’消失掉
ax.spines['top'].set_color('none')  # 设置上‘脊梁’消失掉
plt.plot(x, s, color='green')
for i in range(y.size):
    plt.plot([x[i], x[i]], [s[i], 0], color='#666666', linestyle='--')

plt.show()

傅里叶变换

参考：https://blog.csdn.net/l494926429/article/details/51818012

正弦是一种自然摆动，象征着平滑

正弦运动是变速的：开始快，慢慢减速直至停止，然后又开始加速。如同弹簧的弹跳，钟摆的摆动，琴弦的振动。

v2-43f1a1684b302373b2c42a7fcb23198f_b

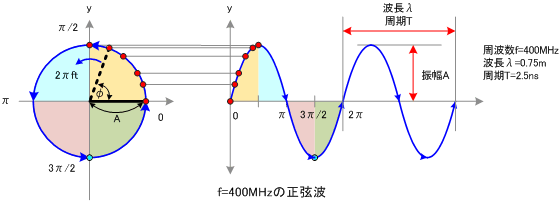
正弦波可看做是一个圆周运动在一条直线上的投影。

x(t) = A sin(2 π f t + φ) = A sin(ω t + φ)

  • A——振幅
  • (ωt+φ)——相位
  • φ——初相
  • ω——角速度，在单位时间内所走的弧度，ω=2π/T=2 π f
  • T——周期
  • f——频率，单位时间内完成周期性变化的次数，f=1/T
  • λ——波长，一个变化周期内传播的距离叫做波长，λ=vT，v指波速，电磁波传播速度与光速相同，为10^8米每秒

bcb52578f6419c3350bb31edccfc3838

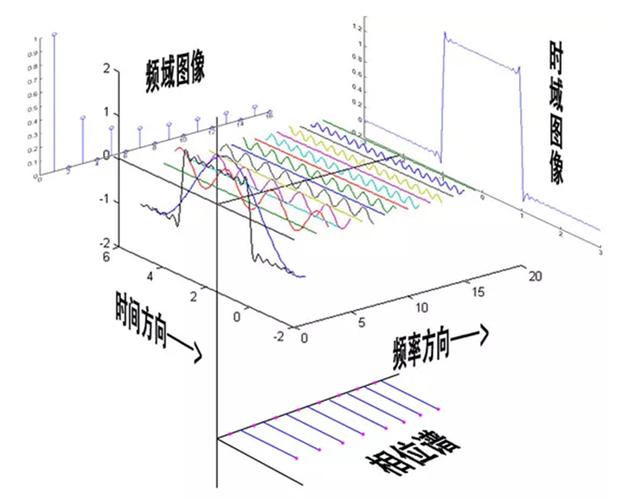
傅里叶变换是一种信号分析方法，可以把时域信号转为频域信号，让我们对信号的构成和特点进行深入的、定量的研究。把信号通过频谱的方式(包括幅值谱、相位谱和功率谱)进行准确的、定量的描述。

傅里叶变换的核心在于任何信号都可以表示成不同振幅，不同相位正弦信号的叠加。

4bed2e738bd4b31c1d60e341d143c7799f2ff80c

图中最前面黑色的线就是所有正弦波叠加而成的总和，也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。这些正弦波按照频率从低到高从前向后排列开来，而每一个波的振幅都是不同的。每两个正弦波之间都还有一条直线，那并不是分割线，而是振幅为 0 的正弦波！也就是说，为了组成特殊的曲线，有些正弦波成分是不需要的。

频域图像从侧面看。在频谱中，偶数项的振幅都是0，也就对应了图中的彩色直线。振幅为 0 的正弦波。

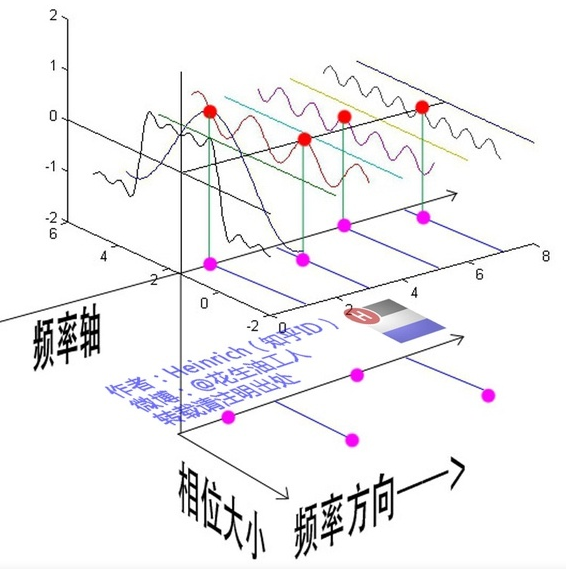
频谱并没有包含时域中全部的信息。因为频谱只代表每一个对应的正弦波的振幅是多少，而没有提到相位。基础的正弦波A.sin(wt+θ)中，振幅，频率，相位缺一不可，不同相位决定了波的位置，所以对于频域分析，仅仅有频谱（振幅谱）是不够的，我们还需要一个相位谱。

相位谱图像从上面看。

image-20220309213034209

图中红点是距离频率轴最近的波峰，紫色为投影下的点。但是这些紫色的点是投影在时间轴上的，只标注了波峰距离频率轴的时间差，并不是相位。将时间差除周期再乘2Pi，就得到了相位差。

Scipy包含FFT实现，更底层和高效。

Numpy也有一个FFT(numpy.fft)实现。

1
2
3
4
fft.fft(a, n=None, axis=- 1, norm=None)
# norm = {“backward”, “ortho”, “forward”}
# 指示前向/后向变换对的哪个方向被缩放以及使用什么归一化因子
# 默认backward
1
fft.ifft(a, n=None, axis=- 1, norm=None)

测试

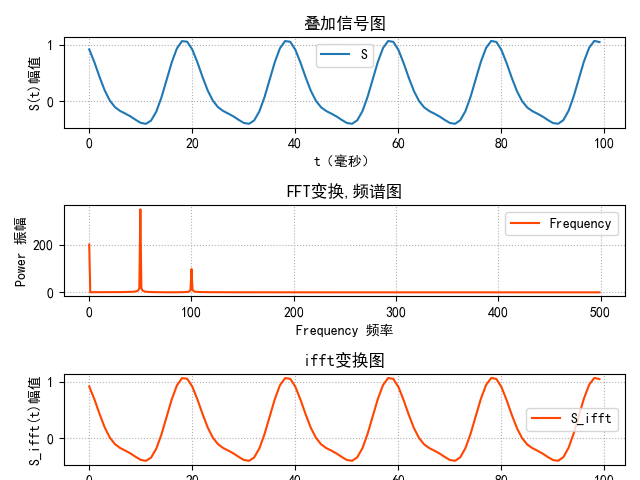
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import matplotlib.pyplot as plt
import numpy as np
import numpy.fft as fft

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示符号

# 采样点选择1000个，因为设置的信号频率分量最高为100赫兹，根据采样定理知采样频率要大于信号频率2倍
t = np.linspace(0, 1, 1000)

# 直流分量是0.2，以及两个余弦函数的叠加，余弦函数的幅值分别为0.7和0.2，频率分别为50和100，初相位分别为20度和70度
S = 0.2 + 0.7 * np.cos(2 * np.pi * 50 * t + 20 / 180 * np.pi) + 0.2 * np.cos(2 * np.pi * 100 * t + 70 / 180 * np.pi)

complex_array = fft.fft(S)  # 傅里叶变换后的复数数组,变换之后的结果数据长度和原始采样信号是一样的
print(complex_array.shape)
print(complex_array.dtype)
print(complex_array[1])
# 复数的模(绝对值)代表的是振幅，复数的辐角代表初相位
pows = np.abs(complex_array)  # 振幅

#################################
# 绘制数据采样图
plt.subplot(3,1,1)
plt.grid(linestyle=':') # 绘制网格线
plt.plot(1000 * t[:100], S[:100], label='S')  # y是1000个相加后的正弦序列
plt.xlabel("t（毫秒）")
plt.ylabel("S(t)幅值")
plt.title("叠加信号图")
plt.legend()

###################################
# 绘制频谱图
# np.fft.fftfreq(采样数量, 采样周期)　　通过采样数与采样周期得到时域序列经过傅里叶变换后的频率序列
freqs = fft.fftfreq(t.size, 1/1000)
print(freqs.shape)
# 复数的模为信号的振幅（能量大小）
plt.subplot(3,1,2)
plt.title('FFT变换,频谱图')
plt.xlabel('Frequency 频率')
plt.ylabel('Power 振幅')
plt.tick_params(labelsize=10)  # 刻度线样式
plt.grid(linestyle=':')
plt.plot(freqs[freqs >= 0], pows[freqs >= 0], c='orangered', label='Frequency')
plt.legend()
plt.tight_layout()
# 频谱图中，第一个峰值（频率位置）的模是常数项A1的N倍，N为采样点，本程序显示为0.2*1000
# 第二个峰值（频率位置）的模是A2的N/2倍，N为采样点，0.7*500
# 第三个峰值（频率位置）的模是A3的N/2倍，N为采样点，0.2*500
# 第四个峰值（频率位置）的模是A4的N/2倍，N为采样点...
# 一般是不显示这个常数项的，取 freqs > 0即可
# 频谱图中频率最低的元素称为基频，具有最高幅度的称为主频
# 频谱图中只显示一半采样频率的数据，就是因为奎纳斯定理采样频率大于信号频率的2倍

###################################

plt.subplot(3,1,3)
S_ifft = fft.ifft(complex_array) # 傅里叶逆变换

plt.plot(1000 * t[:100], S_ifft[:100], label='S_ifft', color='orangered')
plt.xlabel("t（毫秒）")
plt.ylabel("S_ifft(t)幅值")
plt.title("ifft变换图")
plt.grid(linestyle=':')
plt.legend()

plt.show()

效果

Figue_1

数据滤波

数据滤波的作用：

1、将有用的信号与噪声分离，提高信号的抗干扰性及信噪比；

2、滤掉不感兴趣的频率成分，提高分析精度；

3、从复杂频率成分中分离出单一的频率分量。

频域滤波

通过时域转换为频域，在频域信号中去除相应频域信号，最后在逆转换还原为时域型号。

使用傅里叶变换将时域信号转为频域信号可以很容易地对数据进行滤波处理。

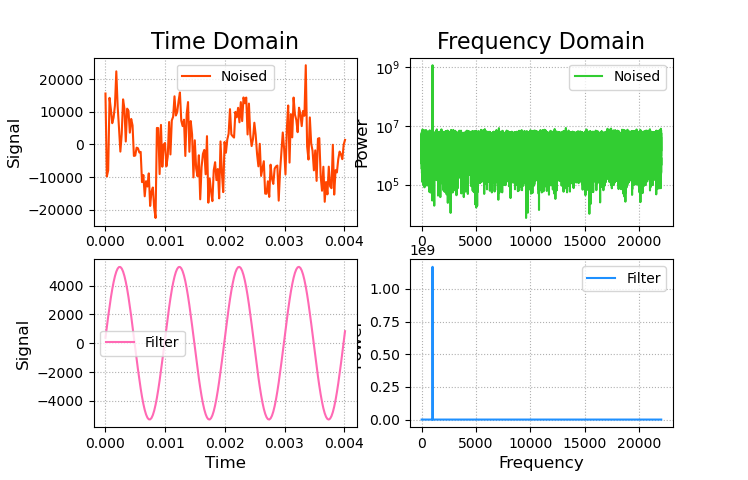
这里以一个音频信号处理为例，将包含噪声的音频信号经过傅里叶变换，只保留最大频率信号，在经过逆变换还原。可以发现音频信号变得平滑，噪声也消失了。

Filter

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
import numpy as np
import numpy.fft as nf
import scipy.io.wavfile as wf  # wav数据读取
import matplotlib.pyplot as plt

# 读取包含噪音的音频文件
sample_rate, noised_sigs = wf.read('noised.wav')
print(sample_rate)  # sample_rate：采样率44100
print(noised_sigs.shape)  # noised_sigs:存储音频中每个采样点的采样位移(220500,)
times = np.arange(noised_sigs.size) / sample_rate

# 绘制音频信号图像
plt.figure('Filter')
plt.subplot(221)
plt.title('Time Domain', fontsize=16)
plt.ylabel('Signal', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(times[:178], noised_sigs[:178], c='orangered', label='Noised')
plt.legend()

# 傅里叶变换后，绘制频域图像
freqs = nf.fftfreq(times.size, times[1] - times[0])
complex_array = nf.fft(noised_sigs)
pows = np.abs(complex_array)

plt.subplot(222)
plt.title('Frequency Domain', fontsize=16)
plt.ylabel('Power', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
# 指数增长坐标画图
plt.semilogy(freqs[freqs > 0], pows[freqs > 0], c='limegreen', label='Noised')
plt.legend()

# 寻找能量最大的频率值
fund_freq = freqs[pows.argmax()]
# where函数寻找那些需要抹掉的复数的索引
noised_indices = np.where(freqs != fund_freq)
# 复制一个复数数组的副本，避免污染原始数据
filter_complex_array = complex_array.copy()
filter_complex_array[noised_indices] = 0
filter_pows = np.abs(filter_complex_array)

plt.subplot(224)
plt.xlabel('Frequency', fontsize=12)
plt.ylabel('Power', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs >= 0], filter_pows[freqs >= 0], c='dodgerblue', label='Filter')
plt.legend()

filter_sigs = nf.ifft(filter_complex_array).real
plt.subplot(223)
plt.xlabel('Time', fontsize=12)
plt.ylabel('Signal', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(times[:178], filter_sigs[:178], c='hotpink', label='Filter')  # 滤波后的信号周期为0.001s,频率为1000Hz
plt.legend()

# 音乐频率范围约为20Hz---20KHz，人的声音频率范围约为300Hz---3.4KHz。但人能听到的最高频率是15KHz
# 人声:男:低音82~392Hz，基准音区64~523Hz
# 男中音123~493Hz，男高音164~698Hz
# 女:低音82~392Hz，基准音区160~1200Hz
# 女中音123~493Hz，女高音220~1.1KHz

# 生成音频文件
wf.write('filter.wav', sample_rate, filter_sigs)
plt.show()

plt.show()

时域滤波

参考：滤波器（FIR与IIR）

滤波器通过减小或放大某些频率来改变时间信号的频率成分。

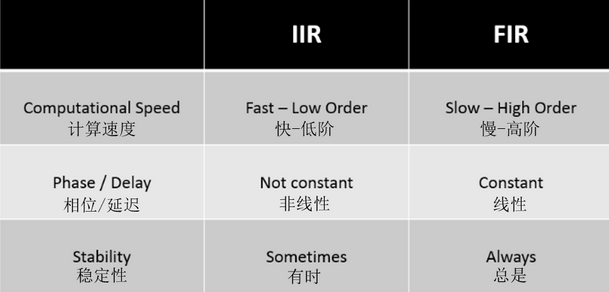
数据滤波的时域方法是对信号离散数据进行差分方程数学运算来达到滤波的目的。经典数字滤波器实现方法主要有两种。一种是IIR数字滤波器，称为无限长冲激响应滤波器；另一种是FIR滤波器，称为有限长冲激响应滤波器。

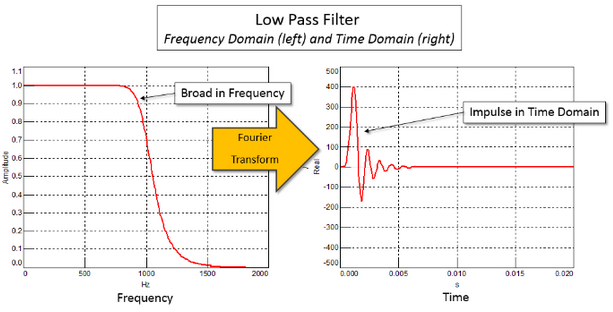
其中脉冲响应”是指滤波器在时域中的外观。滤波器通常具有较宽的频率响应，其对应于时域中的短持续时间脉冲。

image-20220311103739762

无限长冲激响应IIR数字滤波器（Infinite Impuloe Response Digital Filter）的特征是具有无限持续时间的冲激响应，由于这种滤波器一般需要用递归模型来实现，因而又称为递归滤波器。因为IIR滤波器不仅用了输入有限项计算，而且把滤波器以前输出的有限项重新输入再计算，这在工程上称为反馈。

IIR数字滤波器的设计通常借助于模拟滤波器原型，再将模拟滤波器转换成数字滤波器。模拟滤波器的设计较为成熟，既有完整的设计公式，还有较为完整的可供查询的图表，因此，充分利用这些已有的资源无疑会给数字滤波器的设计带来很多便利。

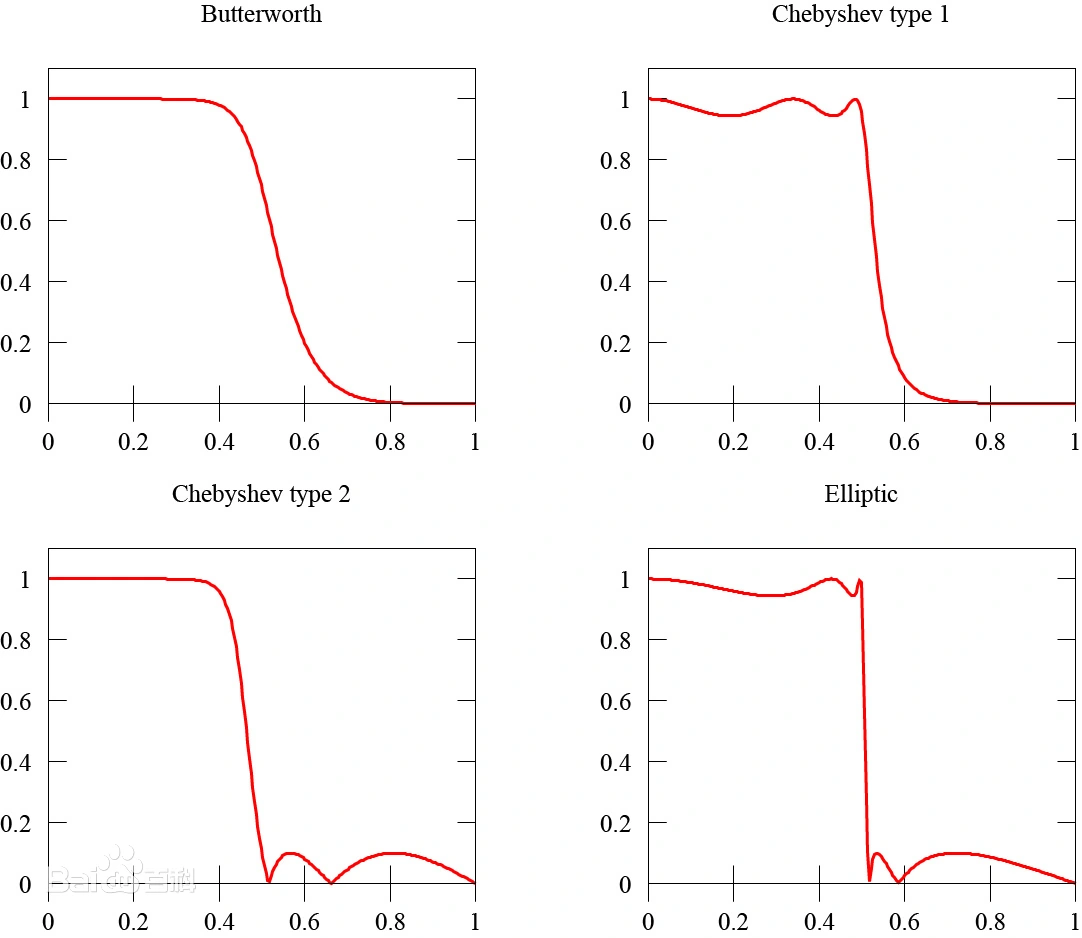
常用的模拟低通滤波器的原型产生函数有==巴特沃斯滤波器原型、切比雪夫1型和2型滤波器原型、椭圆滤波器原型、贝塞尔（Bessel）滤波器原型==等。

77094b36acaf2eddb4e523878c1001e939019343

有限长冲激响应FIR数字滤波器（Finite Impuloe Response Digital Filter）的特征是冲激响应只能延续一定时间，在工程实际应用中主要采用非递归的算法来实现。

优缺点对比：

image-20220311104110602

  • 理想滤波器

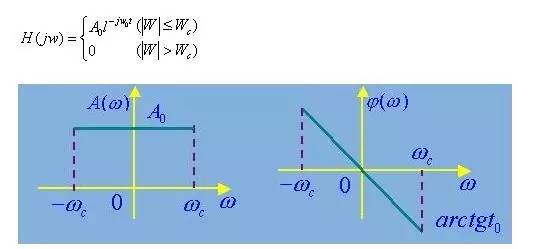
使通带内信号的幅值和相位都不失真，阻喧内的频率成分都衰减为零的滤波器，其通带和阻带之间有明显的分界线。

如理想低通滤波器的频率响应函数为：

img

  • 实际滤波器

img

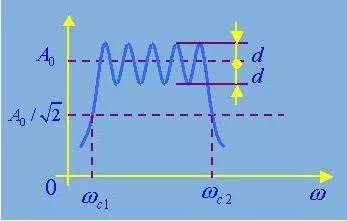
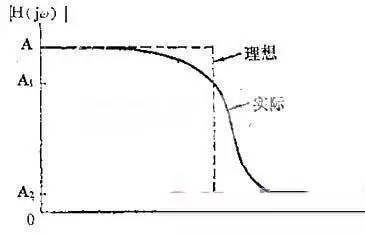
理想滤波器是不存在的，在实际滤波器的幅频特性图中，通带和阻带之间应没有严格的界限。在通带和阻带之间存在一个过渡带。在过渡带内的频率成分不会被完全抑制，只会受到不同程度的衰减。

当然，希望过渡带越窄越好，也就是希望对通带外的频率成分衰减得越快、越多越好。因此，在设计实际滤波器时，总是通过各种方法使其尽量逼近理想滤波器。

img

如上理想带通和实际带通滤波器的幅频特性图可见，理想滤波器的特性只需用截止频率描述，而实际滤波器的特性曲线无明显的转折点，两截止频率之间的幅频特性也非常数，故需用更多参数来描述。

python中可以用lfilter与filtfilt进行滤波。

filtfilt是零相位滤波，在滤波时不会移位信号。由于在所有频率下相位均为零，因此它也是线性相位。及时过滤需要您预测未来，因此不能在“在线”实际应用中使用，仅用于信号记录的离线处理。
lfilter是一种因果时间过滤，类似于现实生活中的电子过滤器。它不能是零相位。它可以是线性相位（对称FIR），但通常不是。通常它会在不同的频率上增加不同的延迟量。

==利用Scipy.signal.filtfilt() 实现信号滤波==

滤波函数：

1
scipy.signal.filtfilt(b, a, x, axis=-1, padtype='odd', padlen=none, method='pad', irlen=none)

输入参数：

b: 滤波器的分子系数向量

a: 滤波器的分母系数向量

x: 要过滤的数据数组。（array型）

这里选用巴特沃斯滤波器（Butterworth filter）滤波器，构造函数：

1
scipy.signal.butter(n, wn, btype='low', analog=false, output='ba')

输入参数：

n: 滤波器的阶数

wn：归一化截止频率。计算公式wn=2*截止频率/采样频率。（注意：根据采样定理，采样频率要大于两倍的信号本身最大的频率，才能还原信号。截止频率一定小于信号本身最大的频率，所以wn一定在0和1之间）。当构造带通滤波器或者带阻滤波器时，wn为长度为2的列表。

btype : 滤波器类型{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’},

output : 输出类型{‘ba’, ‘zpk’, ‘sos’},

输出参数：

b，a: iir滤波器的分子（b）和分母（a）多项式系数向量。output=’ba’

z,p,k: iir滤波器传递函数的零点、极点和系统增益. output= ‘zpk’

sos: iir滤波器的二阶截面表示。output= ‘sos’

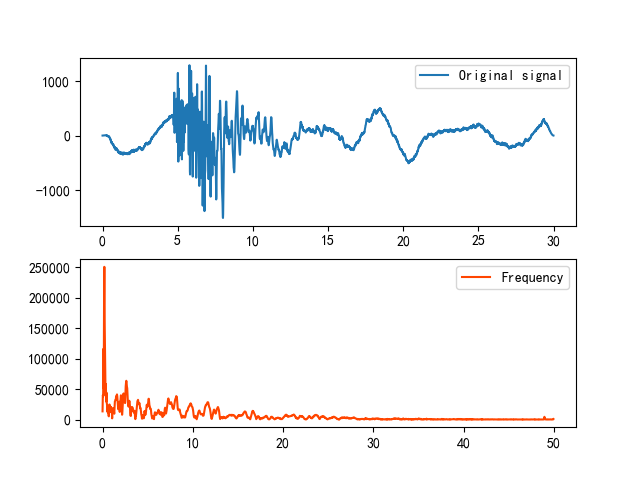
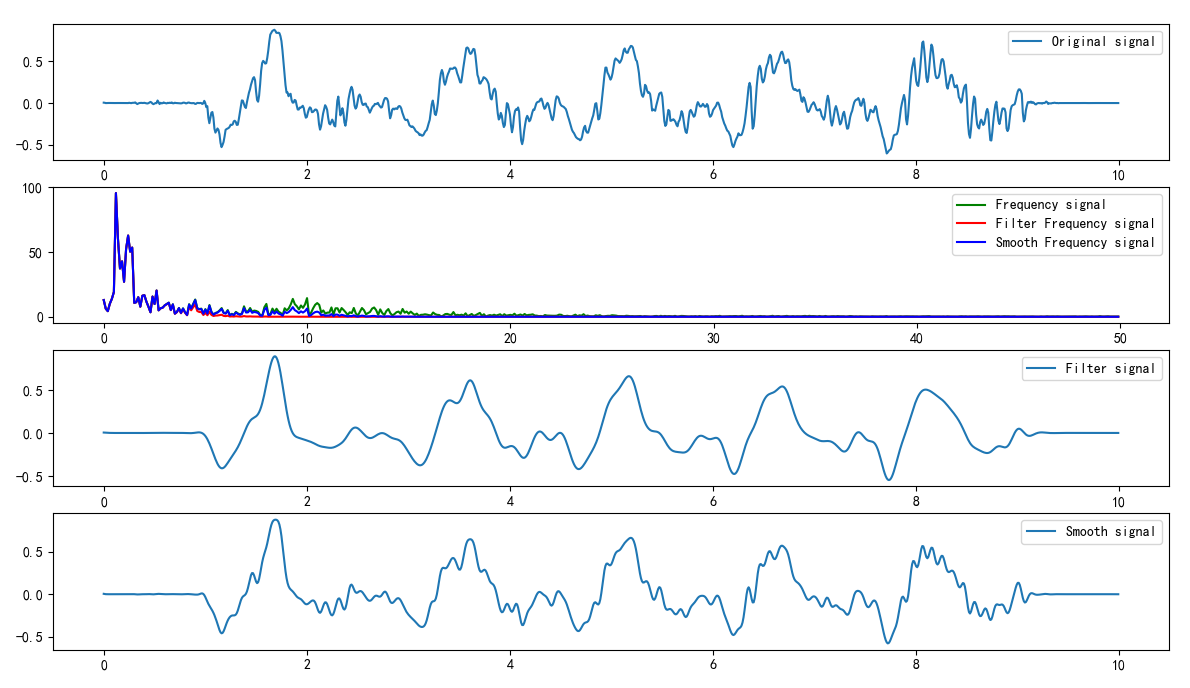
对于如图所示的振动数据：

Figure1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
import numpy.fft as fft
import matplotlib.pyplot as plt
from obspy import read  # 针对地震领域开发的python库

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示符号

###########################
tr = read()[0]

# 原始信号 s1 及对应的时间 t
s1 = tr.data
print(s1.shape)
t = np.arange(len(s1)) * tr.stats.delta  # tr.stats地震元数据，delta采样间隔,0.01s

############################
# 傅里叶变换
complex_array = fft.fft(s1)
pows = np.abs(complex_array)  # 振幅
freqs = fft.fftfreq(t.size, tr.stats.delta) # 采样数量, 采样周期

#############################
plt.subplot(2,1,1)
plt.plot(t, s1, label='Original signal')
plt.legend()

#############################
plt.subplot(2,1,2)
plt.plot(freqs[freqs >= 0], pows[freqs >= 0], c='orangered',label='Frequency')
plt.legend()

plt.show()

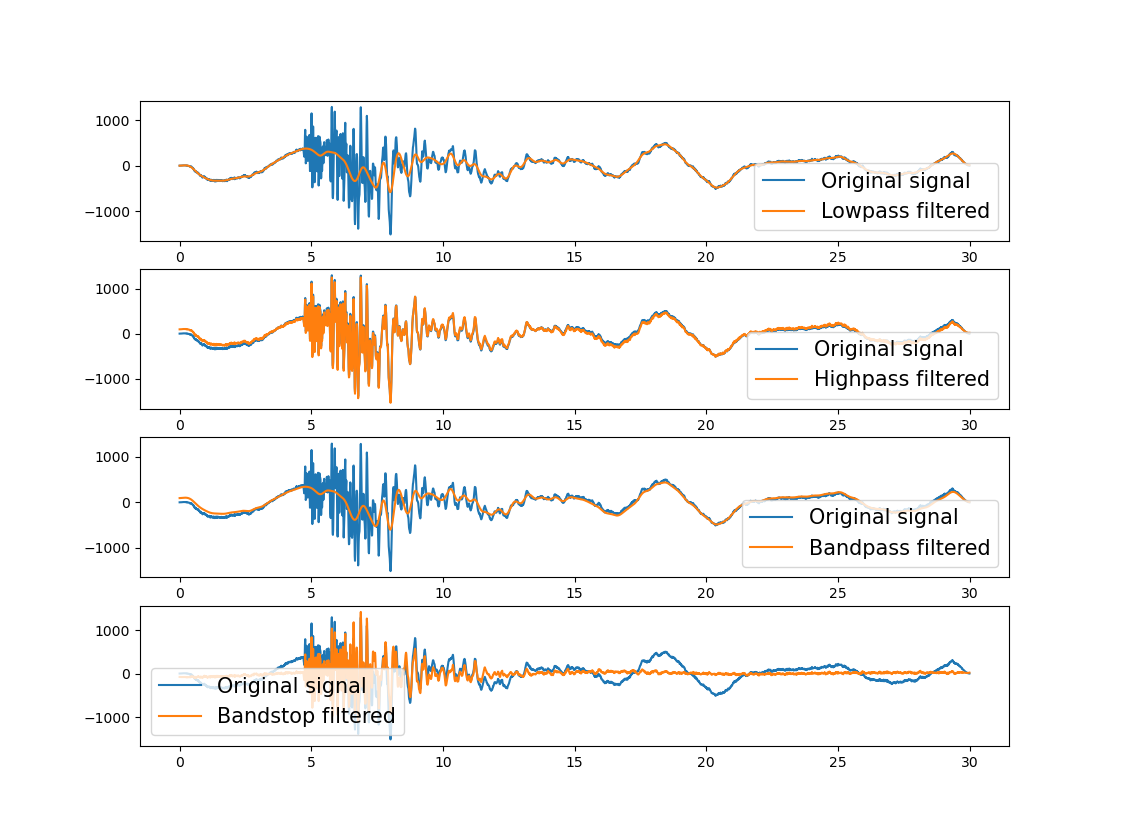
对其进行滤波得到如图所示的结果：

Figure1

根据信号的频谱图可以知道，信号的主频率范围在低频部分。所以低通滤波（<2Hz）效果较好，高通滤波（>0.1Hz）就保留了大部分的高频噪声。带通滤波（>0.1Hz，<2Hz）也有不错的效果，带阻滤波（<0.1Hz， >2Hz）完全偏离原有数据波形。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import numpy as np
import matplotlib.pyplot as plt
from obspy import read  # 针对地震领域开发的python库
from scipy import signal

tr = read()[0]

# 原始信号 s1 及对应的时间 t
s1 = tr.data
print(s1.shape)
t = np.arange(len(s1)) * tr.stats.delta  # tr.stats地震元数据，delta采样间隔,0.01s

fs = 1 / tr.stats.delta  # 采样率 (赫兹)

# 4阶低通滤波
fc = 2  # 截止频率 （赫兹）
b, a = signal.butter(4, 2.0 * fc / fs, btype='lowpass')
s2 = signal.filtfilt(b, a, s1)

# 4阶高通滤波
fc = 0.1  # 截止频率 （赫兹）
b, a = signal.butter(4, 2.0 * fc / fs, btype='highpass')
s3 = signal.filtfilt(b, a, s1)

# 4阶带通滤波
f1 = 0.1
f2 = 2  # 通带的两个截止频率 （赫兹）
b, a = signal.butter(4, [2.0 * f1 / fs, 2.0 * f2 / fs], btype='bandpass')
s4 = signal.filtfilt(b, a, s1)

# 4阶带阻滤波
f1 = 0.1
f2 = 2  # 阻带的两个截止频率
b, a = signal.butter(4, [2.0 * f1 / fs, 2.0 * f2 / fs], btype='bandstop')
s5 = signal.filtfilt(b, a, s1)

# 画图对比
l = 4
plt.figure(figsize=(15, 20))

plt.subplot(l, 1, 1)
plt.plot(t, s1, label='Original signal')
plt.plot(t, s2, label='Lowpass filtered')
plt.legend(fontsize=15)

plt.subplot(l, 1, 2)
plt.plot(t, s1, label='Original signal')
plt.plot(t, s3, label='Highpass filtered')
plt.legend(fontsize=15)

plt.subplot(l, 1, 3)
plt.plot(t, s1, label='Original signal')
plt.plot(t, s4, label='Bandpass filtered')
plt.legend(fontsize=15)

plt.subplot(l, 1, 4)
plt.plot(t, s1, label='Original signal')
plt.plot(t, s5, label='Bandstop filtered')
plt.legend(fontsize=15)
plt.show()

卡尔曼滤波

参考视频：https://www.bilibili.com/video/av203511504?from=search&seid=2691846854868972756&spm_id_from=333.337.0.0

==滤波就是将信号中的噪声滤除，使信号更趋于真实值==。

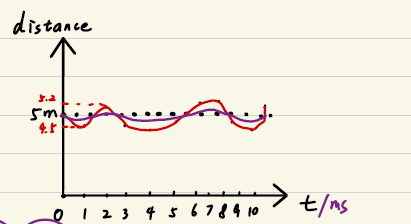
image-20211214150128628

对于上述测距传感器，测量值在一定范围波动，通过平滑滤波可以得到紫色的曲线，明显更接近真实值。

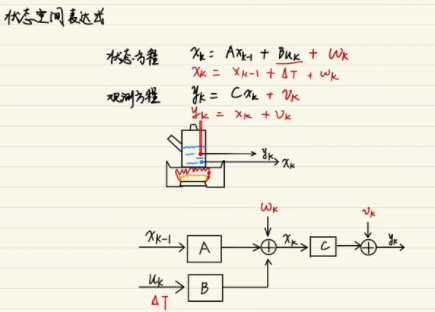
卡尔曼滤波（Kalman filtering）是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。

适用系统：线性高斯系统

  • 线性

    • 叠加性
    • 齐次性

  • 高斯

    噪声满足正态分布

假设你有两个传感器，测的是同一个信号。可是它们每次的读数都不太一样，怎么办？

取平均。

再假设你知道其中贵的那个传感器应该准一些，便宜的那个应该差一些。那有比取平均更好的办法吗？

加权平均。

怎么加权？假设两个传感器的误差都符合正态分布，假设你知道这两个正态分布的方差，用这两个方差值，你可以得到一个“最优”的权重。

接下来，重点来了：假设你只有一个传感器，但是你还有一个数学模型。模型可以帮你算出一个值，但也不是那么准。怎么办？

==把模型算出来的值，和传感器测出的值，（就像两个传感器那样），取加权平均==。

OK，最后一点说明：你的模型其实只是一个步长的，也就是说，知道x(k)，我可以求x(k+1)。问题是x(k)是多少呢？答案：x(k)就是你上一步卡尔曼滤波得到的、所谓加权平均之后的那个、对x在k时刻的最佳估计值。

于是迭代也有了。

这就是卡尔曼滤波。

==kalman滤波用在当测量值与模型预测值均不准确的情况下，用来计算预测真值的一种滤波方法==。

其本质上是一个==数据融合算法==，将具有同样测量目的、来自不同传感器、(可能) 具有不同单位 (unit) 的数据融合在一起，得到一个更精确的目的测量值。

image-20220310100249254

过程噪声Wk属于正态分布N（0；Qk）

观测误差Vk符合正态分布N（0；Rk）

统称为高斯白噪声。

GPS检测位置，检测到车子开了1000m，有一个误差Vk

车在路上行驶，5m/s，1s应该行驶5m，但是可能有顺风和逆风，存在一个误差Wk

image-20211214105503201

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import cv2
import numpy as np

pos = np.array([
    [10, 50],
    [12, 49],
    [11, 52],
    [13, 52.2],
    [12.9, 50]], np.float32)  # 位置数据

'''
它有3个输入参数，dynam_params：状态空间的维数，这里为2；measure_param：测量值的维数，这里也为2;
 control_params：控制向量的维数，默认为0。由于这里该模型中并没有控制变量，因此也为0。
'''
kalman = cv2.KalmanFilter(2, 2)

kalman.measurementMatrix = np.array([[1, 0], [0, 1]], np.float32)  # 观测转移矩阵
kalman.transitionMatrix = np.array([[1, 0], [0, 1]], np.float32)  # 状态转移矩阵
kalman.processNoiseCov = np.array([[1, 0], [0, 1]], np.float32) * 1e-3  # 过程噪声的协方差
kalman.measurementNoiseCov = np.array([[1, 0], [0, 1]], np.float32) * 0.01  # 测量噪声的协方差

'''
kalman.measurementNoiseCov为测量系统的协方差矩阵，方差越小，预测结果越接近测量值
kalman.processNoiseCov为模型系统的噪声，噪声越大，预测结果越不稳定，越容易接近模型系统预测值，
且单步变化越大，相反，若噪声小，则预测结果与上个计算结果相差不大。
'''

kalman.statePre = np.array([[6], [6]], np.float32)

for i in range(len(pos)):  # 迭代过程
    mes = np.reshape(pos[i, :], (2, 1))

    x = kalman.correct(mes)

    y = kalman.predict()

    print(kalman.statePost[0], kalman.statePost[1])
    print(kalman.statePre[0], kalman.statePre[1])
    print('measurement:\t', mes[0], mes[1])
    print('correct:\t', x[0], x[1])
    print('predict:\t', y[0], y[1])
    print('=' * 30)

数据平滑

平滑是滤波实现的一种方法，平滑叫平滑滤波更确切。

平滑就是去掉信号中没必要的快速起伏的成份，让信号看起来更光滑。本质上就是去掉高频分量。与低通滤波相似。

如果你去的噪音是跟信号完全不同的频率成份，就可以只用滤波的方法。比如说，你的信号是低频，噪音是高频，那一个简简单单的低通滤波器就妥妥的。但是可能会经常会遇到噪音的频率成份和信号频率成份重合在一起。滤波的方法是不能用了。那么这个时候，你就必须的借助一些更高级的方法，比如说，自适应滤波，小波变换等等等等。

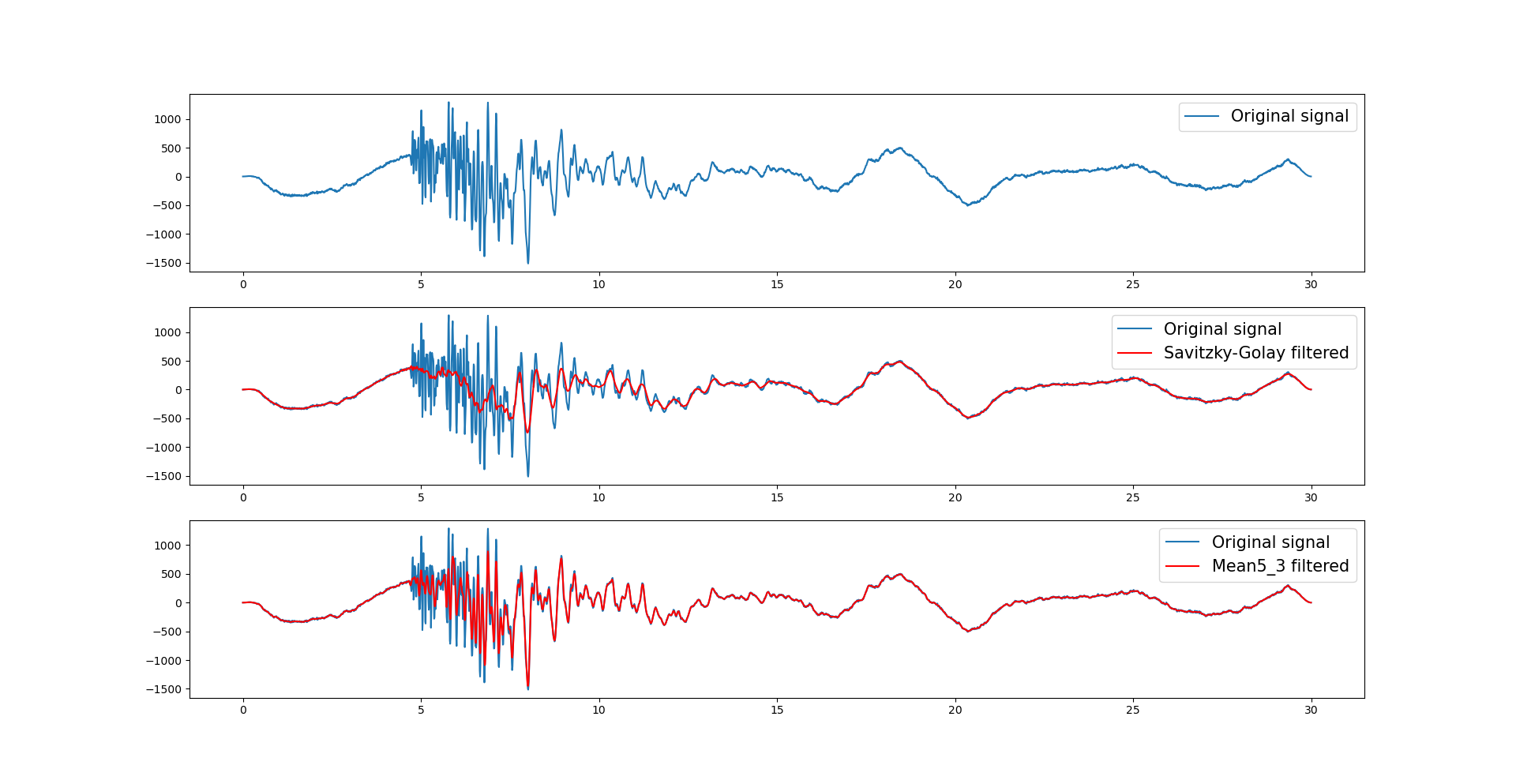
下图是低通滤波和五点三次平滑的效果图：

image-20220311113059133

滑动平均滤波

滑动平均滤波法是把连续取N个采样值看成一个队列 ，队列的长度固定为N ，每次采样到一个新数据放入队尾，并扔掉原来队首的一次数据(先进先出原则) ，把队列中的N个数据进行算术平均运算，就可获得新的滤波结果。

优点： 对周期性干扰有良好的抑制作用，平滑度高 适用于高频振荡的系统

缺点： 灵敏度低 对偶然出现的脉冲性干扰的抑制作用较差

1
numpy.convolve(a, v, mode=‘full')

参数：
　　a:(N,)输入的一维数组
　　v:(M,)输入的第二个一维数组
　　mode:{‘full’, ‘valid’, ‘same’}参数可选
　　　　‘full’　默认值，返回每一个卷积值，长度是N+M-1,在卷积的边缘处，信号不重叠，存在边际效应。
　　　　‘same’　返回的数组长度为max(M, N),==边际效应依旧存在==。
　　　　‘valid’ 　返回的数组长度为max(M,N)-min(M,N)+1,此时返回的是完全重叠的点。边缘的点无效。

1
2
def np_move_avg(a,n,mode="same"):
  return(np.convolve(a, np.ones(n)/n, mode=mode))  # 算术平均值是(x_1 + x_2 + ... + x_N) / N，所以相应的内核是(1/N, 1/N, ..., 1/N)，这正是我们通过使用得到的np.ones(N)/N
1
2
3
4
5
6
7
8
9
10
import numpy as np

tes = np.array([1, 2, 3])
weight = np.ones(2) / 2
result = np.convolve(tes, weight, mode='full')  # [0.5 1.5 2.5 1.5]
print(result)
result = np.convolve(tes, weight, mode='same')  # [0.5 1.5 2.5]
print(result)
result = np.convolve(tes, weight, mode='vaild')  # [1.5 2.5]
print(result)

Savitzky-Golay平滑滤波

SG平滑算法是由Savizkg和Golag提出来的。基于最小二乘原理的多项式平滑算法，也称卷积平滑。其优于滑动平均滤波。

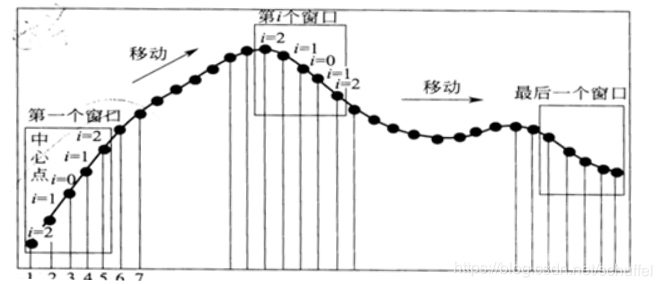
使用五点平滑算法来说明平滑过程：

1433446-20190904203350697-1466434879

把信号一段区间的等波长间隔的5个点记为X集合，多项式平滑就是利用在波长点为Xm-2,Xm-1,Xm,Xm+1,Xm+2的数据的多项式拟合值来取代Xm,，然后依次移动，直到把信号遍历完。（==滑动窗口不能为偶数，且n大于k==）

image-20211210195404225

五点三次平滑

五点三次滤波实际上是略微改进之后的Savitzky-Golay滤波器。

image-20220308154408256

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import numpy as np
import matplotlib.pyplot as plt
from obspy import read  # 针对地震领域开发的python库
from scipy.signal import savgol_filter as sgolay

tr = read()[0]

# 原始信号 s1 及对应的时间 t
s1 = tr.data
# print(tr.stats)
t = np.arange(len(s1)) * tr.stats.delta  # tr.stats地震元数据，delta采样间隔,0.01s

# Savitsky-Golay 平滑滤波
s2 = sgolay(s1, 51, 3)  # 原始数据，滑动窗口大小，拟合多项式的次数


# 5点3次平滑就是用3次多项式和5个数据进行拟合
def Mean5_3(a, m):  # a为输入的一维信号,m为进行多少遍平滑，这是对Savitsky-Golay 平滑滤波的改进,可以进行多遍平滑
    n = a.size
    b = np.empty(n)
    for i in range(m):
        b[0] = (69 * a[0] + 4 * (a[1] + a[3]) - 6 * a[2] - a[4]) / 70
        b[1] = (2 * (a[0] + a[4]) + 27 * a[1] + 12 * a[2] - 8 * a[3]) / 35
        for j in range(2, n - 2, 1):
            b[j] = (-3 * (a[j - 2] + a[j + 2]) + 12 * (a[j - 1] + a[j + 1]) + 17 * a[j]) / 35
        b[n - 2] = (2 * (a[n - 1] + a[n - 5]) + 27 * a[n - 2] + 12 * a[n - 3] - 8 * a[n - 4]) / 35
        b[n - 1] = (69 * a[n - 1] + 4 * (a[n - 2] + a[n - 4]) - 6 * a[n - 3] - a[n - 5]) / 70
        a = b
    return b


s3 = Mean5_3(s1, 50)

plt.subplot(311)
plt.plot(t, s1, label='Original signal')
plt.legend(fontsize=15)

plt.subplot(312)
plt.plot(t, s1, label='Original signal')
plt.plot(t, s2, c='red', label='Savitzky-Golay filtered')
plt.legend(fontsize=15)

plt.subplot(313)
plt.plot(t, s1, label='Original signal')
plt.plot(t, s3, c='red', label='Mean5_3 filtered')
plt.legend(fontsize=15)

plt.show()

Figure_1

去趋势项

参考：https://blog.csdn.net/pengchen_wuhan/article/details/118058489

在振动测试过程中，传感器或采集设备由于自身性能问题或受环境干扰（如温度、供电等影响），容易产生零漂，而偏离基线，偏离基线的大小甚至还会随时间变化。偏离基线随时间变化的过程称之为信号的趋势项。信号的趋势线将直接影响信号分析的准确性，应该将其消除。常用的去除趋势项的方法是最小二乘法。

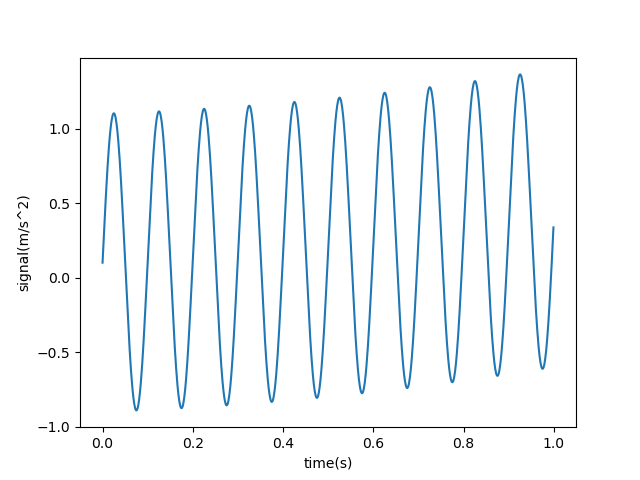
以下实验首先构造包含常数趋势项，线性趋势项和二次曲线趋势项的数据。

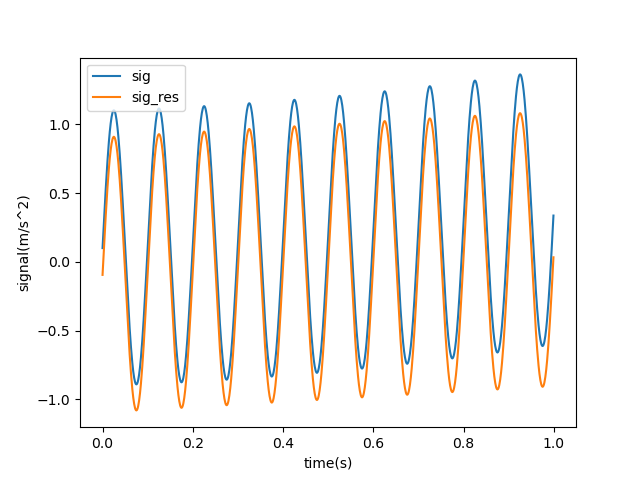
Filter

去趋势项的结果如下：

Filter

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
# 导入模块
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# 构造模拟信号
fre = 10 # 信号的频率为10
t = np.arange(0, 1, 0.001)
sig = np.sin(2 * np.pi * fre * t) + 0.1 + 0.1 * t + 0.2 * t ** 2  # 包含常数趋势项，线性趋势项和二次曲线趋势项
t = t.reshape(-1, 1) # -1表示自动计算，把数组编程1000行1列的二维数组
sig = sig.reshape(-1, 1) 

#########################################
# 展示模拟信号
plt.plot(t, sig)
plt.xlabel('time(s)')
plt.ylabel('signal(m/s^2)')
plt.show()

########################################
# 构造去除趋势项函数
def trend_remove(t, sig, degree):
    # 构造多项式回归模型
    poly_reg = Pipeline([ # Pieline可以将许多算法模型串联起来
        ('poly', PolynomialFeatures(degree=degree)), # PolynomialFeatures用于生成多项式，degree默认为2，多项式阶次
        ('lin_reg', LinearRegression(fit_intercept=False))]) # LinearRegression线性回归模型
    # 训练多项式回归模型（即求待定系数）
    poly_reg.fit(t, sig) # fit方法用于训练模型
    # 去除趋势项
    sig_predict = poly_reg.predict(t) # predict进行模型预测
    sig_res = sig - sig_predict
    # 输出趋势项待定系数
    model = poly_reg.named_steps['lin_reg']
    print('趋势项待定系数为：')
    print(model.coef_[0])
    # 返回去趋势项结果
    return sig_res

########################################
sig_res = trend_remove(t, sig, 2)

# 展示去除趋势项后的信号
plt.plot(t, sig)
plt.plot(t, sig_res)
plt.xlabel('time(s)')
plt.ylabel('signal(m/s^2)')
plt.legend(['sig','sig_res'])
plt.show()